
Контрольная работа 1.
ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
Введите номер задачи и нажмите кнопку "Решение", или решите задачу на основании нижепредставленных формул.
Основные формулы по курсу "Механика"
Кинематические уравнения движения материальной точки (центра масс твёрдого тела) вдоль оси \(x\) $$ x = f(t), $$
где \(f(t)\) — некоторая функция времени.
Проекция средней скорости на ось \(x\) $$ \left< v_x \right>= {\Delta x \over \Delta t}. $$
Средняя путевая скорость \(x\) $$ \left< v \right>= {\Delta s \over \Delta t}, $$
где \(\Delta s\) — путь, пройденный точкой за интервал времени \(\Delta t\). Путь \(\Delta s\) в отличие от разности координат \(\Delta x = x_2-x_1\) не может убывать и принимать отрицательные значения, т.е. \(\Delta s\ge0\).
Проекция мгновенной скорости на ось \(x\) $$ v_x = {d x \over d t}. $$
Проекция среднего ускорения на ось \(x\) $$ \left< a_x \right>= {\Delta v_x \over \Delta t}. $$
Проекция мгновенного ускорения на ось \(x\) $$ a_x = {d v_x \over d t}. $$
Кинематическое уравнение движения материальной точки по окружности $$ \varphi=f(t), \qquad \qquad r=R=const. $$
Модуль угловой скорости $$ \omega = {d\varphi \over d t}. $$
Модуль углового ускорения $$ \varepsilon = {d\omega \over d t}. $$
Связь между модулями линейных и угловых величин, характеризующих движение точки по окружности:$$ v=\omega\cdot R, \qquad \qquad a_\tau = \varepsilon \cdot R, \qquad \qquad a_n= \omega^2 \cdot R, $$ где \(v\) — модуль линейной скорости; \(a_\tau\) и \(a_n\) — модули тангенциального и нормального ускорений; \(\omega\) — модуль угловой скорости; \(\varepsilon\) — модуль углового ускорения; \(R\) — радиус окружности.
Модуль полного ускорения$$ a=\sqrt{a_\tau^2+a_n^2}, \qquad или \qquad a=R\sqrt{\varepsilon^2+\omega^4}.$$
Угол между полным \(a\) и нормальным \(a_n\) ускорениями $$ \alpha =arccos(a_n / a). $$
Кинематическое уравнения гармонических колебаний материальной точки$$ x=Acos(\omega t+\varphi), $$ где \(x\) — смещение; \(A\) — амплитуда колебаний; \(\omega\) — угловая или циклическая частота; \(\varphi\) — начальная фаза.
Скорость и ускорение материальной точки, совершающей гармонические колебания:$$ v=-A\omega sin(\omega t+\varphi); \qquad \qquad a=-A\omega^2 cos(\omega t+\varphi). $$
Сложение гармонических колебаний одного направления и одинаковой частоты:
а) амплитуда результирующего колебания $$ A=\sqrt{A_1^2+A_2^2+2A_1A_2cos(\varphi_2-\varphi_1)}; $$ б) начальная фаза результирующего колебания$$ \varphi=arctg{{A_1sin\varphi_1+A_2sin\varphi_2} \over {A_1cos\varphi_1+A_2cos\varphi_2}}. $$
Траектория точки, участвующей в двух взаимно перпендикулярных колебаниях,
$$ x=A_1cos\omega t; \qquad \qquad y=A_2cos(\omega t+\varphi). $$ a) \( x={A_2 \over A_1}x, \) если разность фаз \(\varphi=0;\)
б) \( x=-{A_2 \over A_1}x, \) если разность фаз \(\varphi=\pi\) или \(\varphi=-\pi; \)
в) \({x^2 \over A_1^2}+{y^2 \over A_2^2}=1\), если разность фаз \(\varphi={\pi \over 2}\) или \(\varphi=-{\pi \over 2}\).
Уравнение плоской бегущей волны $$ y=Acos\omega \left( t-\frac x v\right),$$ где \(y\) — смещение любой из точек среды с координатой \(x\) в момент времени \(t\); \(v\) — скорость распространения колебаний в среде.
Связь разности фаз \(\Delta\varphi\) колебаний с расстоянием \(\Delta x\) между точками среды, отсчитанным в направлении распространения колебаний; $$ \Delta\varphi = {{2\pi}\over\lambda}\Delta x, $$ где \(\lambda\) — длина волны.
Импульс материальной точки массой \(m\), движущейся со скоростью \(\vec v\), $$ \vec p=m\vec v. $$
Второй закон Ньютона $$ d\vec p=\vec F dt, \qquad или \qquad \vec F =m \vec a, $$ где \(\vec F\) — результирующая сила, действующая на материальную точку; \(\vec a\) — полное ускорение точки.
Силы, рассматриваемые в механике:
а) сила упругости$$ F=-kx,$$где \(k\) — коэффициент упругости (в случае пружины — жёсткость); \(x\) — абсолютная деформация;
б) сила тяжести $$ P=mg,$$где \(g=9,81 {м \over с^2}\) — ускорение свободного падения (напряжённость гравитационного поля);
в) сила гравитационного взаимодействия$$ F=G{{m_1m_2}\over r^2},$$где \(G=6,67\cdot 10^{-11}{кг\over{м\cdot c^2}}\) — гравитационная постоянная; \(m_1\) и \(m_2\) — массы взаимодействующих тел; \(r\) — расстояние между телами (тела рассматриваются как материальные точки) или между центрами тел, если тела имееют шарообразнную форму, как, например, планеты и звёзды. В случае гравитационного взаимодействия силу можно выразить также через напряжённость \(\vec g\) гравитационного поля:$$ \vec F=m \vec g;$$
г) сила трения (скольжения) $$ F=\mu N,$$ где \(\mu \) — коэффициент трения; \(N\) — сила нормального давления (реакция опоры). Сила трения покоя определяется как сила, противоположная равнодействующей остальных сил, действующих на тело.
Закон сохранения импульса$$ \sum_{i=1}^n{p_i}=const, $$ или для двух тел \(n=2\)$$m_1v_1+m_2v_2=m_1u_1+m_2u_2,$$ где \(v_1\) и \(v_2\) — скорости тел в момент времени, принятый за начальный; \(u_1\) и \(u_2\) — скорости тех же тел в момент времени, принятый за конечный.
Кинетическая энергия тела, движущегося поступательно,$$ T={mv^2 \over 2} \qquad или \qquad T={p^2 \over 2m.}$$ Потенциальная энергия:
а) упругодеформированной пружины$$ \Pi={kx^2 \over 2},$$где \(k\) — жёсткость пружины; \(x\) — абсолютная деформация;
б) гравитационного взаимодействия $$ \Pi=-G{{m_1m_2} \over r},$$где \(G\) — гравитационная постоянная; \(m_1\) и \(m_2\) — массы взаимодействующих тел; \(r\) — расстояние между ними (тела рассматриваются как материальные точки) или между центрами тел, если тела имееют шарообразнную форму (звёзды, планеты).
в) тела, находящегося в однородном поле силы тяжести, $$\Pi=mgh, $$где \(m\) — масса тела; \(g\) — ускорение свободного падения; \(h\) —высота тела над уровнем, принятым за нулевой (формула справедлива при условии \(h \lt \lt R \), где \(R=6378 км\) — радиус Земли).
Закон сохранения механической энергии $$E=T+\Pi=const.$$ Работа \(A\), совершаемая результирующей силой, определяется как мера изменения кинетической энергии материальной точки: $$A=\Delta T=T_2-T_1.$$ Работа силы \(\vec F\) на перемещении \(\vec s\) равна скалярному произведению векторов \(\vec F\) и \(\vec s\)$$ A=\left(\vec F,\vec s\right)=F\cdot s \cdot cos\alpha,$$где \(\alpha\) — угол между векторами \(\vec F\) и \(\vec s\).
Мгновенная мощность есть производная работы по времени $$P={dA \over dt}.$$
Средняя мощность или работа, совершаемая в единицу времени, равна $$ \left< P \right> ={A \over t}.$$
Коэффициент полезного действия (КПД): $$ \eta = {A_п \over A_з}\cdot 100 ^o/_o , $$где \(A_п\) — полезная работа, \(A_з\) — затраченная работа.
Основное уравнение динамики вращательного движения относительно неподвижной оси \(z\) $$M_z=J_z\varepsilon,$$ где \(M_z\) — результирующий момент внешних сил относительно оси \(z\), действующих на тело; \(\varepsilon\) — угловое ускорение; \(J_z\) — момент инерции относительно оси вращения.
Моменты инерции некоторых тел массой \(m\) относительно оси \(z\), проходящей через центр масс:
а) стержня длиной \(l\) относительно оси, перпендикулярной стержню,$$J_z={1 \over {12}}ml^2;$$ б) обруча (тонкостенного цилиндра) радиуса \(R\) относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра), $$J_z=mR^2;$$ в) диска (сплошного цилиндра) радиуса \(R\) относительно оси, перпендикулярной плоскости диска (совпадающей с осью цилиндра), $$J_z={1 \over 2}mR^2;$$ г) шара радиуса \(R\) относительно любой оси, проходящей через его центр $$J_z={2 \over 5}mR^2.$$
Момент инерции \(J\) относительно оси, не проходящей через центр масс, определяется теоремой Штейнера $$ J=J_0+ma^2,$$ где \(J_0\) — момент инерции относительно параллельной центральной оси; \(a\) — расстояние между осями.
Проекция на ось \(z\) момента импульса тела, вращающегося относительно неподвижной оси \(z\) с угловой скоростью \(\omega\), $$ L_z=J_z\omega.$$
Закон сохранения момента импульса системы тел, вращающихся вокруг неподвижной оси \(z\),$$J_z\omega=const, $$где \(J_z\) — момент инерции системы тел относительно оси \(z\); \(\omega\) — угловая скорость вращения системы тел относсительно оси \(z\).
Кинетическая энергия тела, вращающегося относительно неподвижной оси \(z\),$$T=\frac12 J_z\omega^2 \qquad или \qquad T={{L_z^2}\over {2J_z}}. $$
101. Тело брошено вертикально вверх с начальной скоростью v0 = 4 м/с. Когда оно достигло верхней точки полета из того же начального пункта, с той же скоростью вертикально вверх было брошено второе тело. На каком расстоянии h от начального пункта встретятся тела? Сопротивлением воздуха пренебречь.
102. Материальная точка движется прямолинейно с ускорением а = 5 м/с2. Определить, на сколько путь, пройденный точкой в n-ю секунду, будет больше пути, пройденного в предыдущую секунду. Принять v0 = 0.
103. Две автомашины движутся по дорогам, угол между которыми α =60˚. Скорость автомашин
104. Материальная точка движется прямолинейно с начальной скоростью v0 = 10 м/с и с постоянным ускорением а = – 5 м/с2. Определить, во сколько раз путь ΔS, пройденный материальной точкой, будет превышать модуль её перемещения Δr спустя t = 4 c после начала отсчета времени.
105. Велосипедист ехал из одного пункта в другой. Первую треть пути он проехал со скоростью v1= 18 км/ч. Далее половину оставшегося времени он ехал со скоростью
106. Тело брошено под углом α=30o к горизонту со скоростью v0=30м/с. Каковы будут нормальное an и тангенциальное aτ ускорения тела через время t=1c после начала движения?
107. Материальная точка движется по окружности с постоянной угловой скоростью
108. Материальная точка движется в плоскости ху согласно уравнениям х = A1 + B1t+C1t2 и у = A2 + B2t + C2t2, где В1 = 7 м/с, C1 = -2 м/с2, В2 = -1 м/с, C2 = 0,2 м/с2. Найти модули скорости и ускорения в момент времени
109. По краю равномерно вращающейся с угловой скоростью ω = 1 рад/с платформы идет человек и обходит платформу за время t = 9,9 с. Каково наибольшее ускорение а движения человека относительно Земли? Принять радиус платформы R = 2 м.
110. Точка движется по окружности радиусом R = 30 см. с постоянным угловым ускорением ε. Определить тангенциальное ускорение ατ точки, если известно, что за время
111. При горизонтальном полете со скоростью v = 250 м/с снаряд массой m = 8 кг разорвался на две части. Большая часть массой m1 = 6 кг получила скорость
112. С тележки, свободно движущейся по горизонтальному пути со скоростью v1 = 3 м/с, в сторону, противоположную движению тележки, прыгает человек, после чего скорость тележки изменилась и стала равной
113. Орудие, жестко закрепленное на железнодорожной платформе, производит выстрел под углом α = 30o к линии горизонта. Определить скорость u2 отката платформы, если снаряд вылетает со скоростью u1 = 480 м/с. Масса платформы с орудием и снарядами
114. Человек массой m1 = 70 кг, бегущий со скоростью v1 = 9 км/ч, догоняет тележку массой
115. Конькобежец, стоя на коньках на льду, бросает камень массой m1 = 2,5 кг под углом
116. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса его m1 = 60 кг, масса тележки m2 = 20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль неё со скоростью (относительно доски) v = 1 м/с? Массой колес и трением пренебречь.
117. Снаряд, летевший со скоростью v = 400 м/с, в верхней точке траектории разорвался на два осколка. Меньший осколок, масса которого составляет 40% от массы снаряда, полетел в противоположном направлении со скоростью u1 = 150 м/с. Определить скорость u2 большего осколка.
118. Две одинаковые лодки массами m=200 кг, каждая (вместе с человеком и грузами, находящимися в лодках) движутся параллельными курсами навстречу друг другу со скоростями v=1 м/c. Когда лодки поравнялись, то с первой лодки на вторую и со второй на первую одновременно перебрасывают грузы массами m1=20 кг. Определить скорости u1 и u2 лодок после перебрасывания грузов.
119. На сколько переместится относительно берега лодка длиной l = 3,5 м и массой
120. Лодка длиной l = 3 м и массой m = 120 кг стоит на спокойной воде. На носу и корме находятся два рыбака массами m1 = 60 кг и m2 = 90 кг. На сколько сдвинется лодка относительно воды, если рыбаки поменяются местами?
121. В деревянный шар массой m1 = 8 кг, подвешенный на нити длиной l = 1,8 м, попадает горизонтально летящая пуля массой m2 = 4 г. С какой скоростью летела пуля, если нить с шаром и застрявшей в нем пулей отклонилась от вертикали на угол α = 3o? Размером шара пренебречь. Удар пули считать прямым, центральным.
122. По небольшому куску мягкого железа, лежащему на наковальне массой m1 = 300 кг, ударяет молот массой m2 = 8 кг. Определить КПД η удара, если удар неупругий. Полезной считать энергию, затраченную на деформацию куска железа.
123. Шар массой m1 = 1 кг движется со скоростью v1 = 4 м/c и сталкивается с шаром массой
124. Шар массой m1 = 3 кг движется со скоростью v1= 2 м/c и сталкивается с покоящимся шаром массой m2 = 5 кг. Какая работа будет совершена при деформации шаров? Удар считать абсолютно неупругим, прямым и центральным.
125. Определить КПД η неупругого удара бойка массой m1 = 0,5 т, падающего на сваю массой
126. Шар массой m1= 4 кг движется со скоростью v1= 5 м/c и сталкивается с шаром массой
127. Из ствола автоматического пистолета вылетела пуля массой m1 = 10 г со скоростью
128. Шар массой m1 = 5 кг движется со скоростью v1 = 1 м/c и сталкивается с покоящимся шаром массой m2 = 2 кг. Определить скорости u1 и u2 шаров после удара. Удар считать абсолютно упругим, прямым, центральным.
129. Из орудия, не имеющего противооткатного устройства, производилась стрельба в горизонтальном направлении. Когда орудие было неподвижно закреплено, снаряд вылетел со скоростью v1=600 м/c, а когда орудию дали возможность свободно откатываться назад, снаряд вылетел со скоростью v2=580 м/c. С какой скоростью откатилось при этом орудие?
130. Шар массой m1=2 кг сталкивается с покоящимся шаром большей массы и при этом теряет 40% кинетической энергии. Определить массу m2 большого шара. Удар считать абсолютно упругим, прямым, центральным.
131. Определить работу растяжения двух соединенных последовательно пружин жесткостями
132. Из шахты глубиной h = 600 м поднимают клеть массой m1 = 3,0 т на канате, каждый метр которого имеет массу m = 1,5 кг. Какая работа А совершается при поднятии клети на поверхность Земли? Каков коэффициент полезного действия η подъемного устройства?
133. Пружина жесткостью k = 500 H/м сжата силой F = 100 H. Определить работу А внешней силы, дополнительно сжимающей пружину ещё на Δl = 2 см.
134. Две пружины жесткостью k1 = 0,5 кН/м и k2 = 1 кН/м скреплены параллельно. Определить потенциальную энергию Π данной системы при абсолютной деформации Δl = 4 см.
135. Какую нужно совершить работу А, чтобы пружину жесткостью k = 800 Н/м, сжатую на
136. Если на верхний конец вертикально расположенной спиральной пружины положить груз, то пружина сожмется на Δl = 3 мм. На сколько сожмет пружину тот же груз, упавший на конец пружины с высоты h = 8 см?
137. Из пружинного пистолета с пружиной жесткостью k = 150 Н/м был произведен выстрел пулей массой m = 8 г. Определить скорость v пули при вылете её из пистолета, если пружина была сжата на Δх = 4 см.
138. Налетев на пружинный буфер, вагон массой m = 16 т, двигавшийся со скоростью
139. Цепь длиной l = 2 м лежит на столе, одним концом свисая со стола. Если длина свешивающейся части превышает 1/3l, то цепь соскальзывает со стола. Определить скорость v цепи в момент её отрыва от стола.
140. Какая работа А должна быть совершена при поднятии с земли материалов для постройки цилиндрической дымоходной трубы высотой h = 40 м, наружным диаметром D = 3,0 м и внутренним диаметром d = 2,0 м? Плотность материала ρ принять равной
141. Шарик массой m = 60 г, привязанный к концу нити длиной l = 1,2 м, вращается с частотой n1 = 2 c-1, опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси до расстояния l2 = 0,6 м. С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь.
142. По касательной к шкиву маховика в виде диска диаметром D = 75 см и массой
143. На обод маховика диаметром D = 60 см намотан шнур, к концу которого привязан груз массой m = 2 кг. Определить момент инерции J маховика, если он, вращаясь равноускоренно под действием силы тяжести груза, за время t = 3 c приобрел угловую скорость ω = 9 рад/с.
144. Нить с привязанными к её концам грузами массами m1 = 50 г и m2 = 60 г перекинута через блок диаметром D = 4 см. Определить момент инерции J блока, если под действием силы тяжести грузов он получил угловое ускорение ε = 1,5 рад/c2. Трением и проскальзыванием нити по блоку пренебречь.
145. Стержень вращается вокруг оси, проходящей через его середину, согласно уравнению φ=At+Bt3, где А = 2 рад/с, В = 0,2 рад/с3. Определить вращающий момент М, действующий на стержень через время t = 2 c после начала вращения, если момент инерции стержня
146. По горизонтальной плоскости катится диск со скоростью v = 8 м/с. Определить коэффициент сопротивления, если диск, будучи предоставленным самому себе, остановился, пройдя путь s = 18 м.
147. Определить момент силы М, который необходимо приложить к блоку, вращающемуся с частотой n = 12 c-1, чтобы он остановился в течение времени Δt = 8 c. Диаметр блока
148. Блок, имеющий форму диска массой m = 0,4 кг, вращается под действием силы натяжения нити, к концам которой подвешены грузы массами m1 = 0,3 кг, m2 = 0,7 кг. Определить силы натяжения Т1 и Т2 нити по обе стороны блока.
149. К краю стола прикреплен блок. Через блок перекинута невесомая и нерастяжимая нить, к концам которой прикреплены грузы. Один груз движется по поверхности стола, а другой – вдоль вертикали вниз. Определить коэффициент f трения между поверхностями груза и стола, если массы каждого груза и масса блока одинаковы и грузы движутся с ускорением а=5,6 м/с2. Проскальзыванием нити по блоку и силой трения, действующей на блок пренебречь.
150. К концам лёгкой и нерастяжимой нити, перекинутой через блок, подвешены грузы массами
151. На скамье Жуковского сидит человек и держит на вытянутых руках гири массой
152. На скамье Жуковского стоит человек и держит в руках стержень вертикально по оси скамьи. Скамья с человеком вращается с угловой скоростью ω1 = 4 рад/с. С какой угловой скоростью ω2 будет вращаться скамья с человеком, если повернуть стержень так, чтобы он занял горизонтальное положение? Суммарный момент инерции человека и скамьи J = 5 кг·м2. Длина стержня l = 1,8 м, масса m = 6 кг. Считать, что центр масс стержня с человеком находится на оси платформы.
153. Платформа в виде диска диаметром 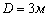 и массой
и массой 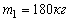 может вращаться вокруг вертикальной оси. С какой угловой скоростью
может вращаться вокруг вертикальной оси. С какой угловой скоростью 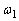 будет вращаться эта платформа, если по её краю пойдёт человек массой
будет вращаться эта платформа, если по её краю пойдёт человек массой 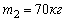 со скоростью
со скоростью 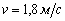 относительно платформы?
относительно платформы?
154. Платформа, имеющая форму диска, может вращаться около вертикальной оси. На краю платформы стоит человек. На какой угол φ повернется платформа, если человек пойдет вдоль платформы и, обойдя её, вернётся в исходную (на платформе) точку? Масса платформы m1 = 280 кг, масса человека m2 = 80 кг.
155. На скамье Жуковского стоит человек и держит в руке за ось велосипедное колесо, вращающееся вокруг своей оси с угловой скоростью ω1 = 25 рад/с. Ось колеса расположена вертикально, и совпадает с осью скамьи Жуковского. С какой скоростью ω2 станет вращаться скамья, если повернуть колесо вокруг горизонтальной оси на угол α=90o? Момент инерции человека и скамьи J равен 2,5 кг·м2, момент инерции колеса J0 =0,5 кг·м2.
156. Однородный стержень длиной l = 1,0 м может свободно вращаться вокруг горизонтальной оси, проходящей через один из его концов. В другой конец абсолютно неупруго ударяет пуля массой m = 7 г, летящая перпендикулярно стержню и его оси. Определить массу М стержня, если в результате попадания пули он отклонится на угол α = 60o. Принять скорость пули
157. На краю платформы в виде диска, вращающейся по инерции вокруг вертикальной оси с частотой n1=8мин-1, стоит человек массой m1=70кг. Когда человек перешел в центр платформы, она стала вращаться с частотой n2=10мин-1. Определить массу m2 платформы. Момент инерции человека рассчитывать как для материальной точки.
158. На краю неподвижной скамьи Жуковского диаметром D = 0,8 м и массой m1 = 6 кг стоит человек массой m2 = 60 кг. С какой угловой скоростью ω начнет вращаться скамья, если человек поймает летящий на него мяч массой m = 0,5 кг? Траектория мяча горизонтальна и проходит на расстоянии r = 0,4 м от скамьи. Скорость мяча v = 5 м/с.
159. Горизонтальная платформа массой m1 = 150 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n = 8 мин-1. Человек массой
160. Однородный стержень длиной l = 1,0 м и массой М = 0,7 кг подвешен на горизонтальной оси, проходящей через конец стержня. В точку, отстоящую от оси на 2/3l, абсолютно упруго ударяет пуля массой m = 5 г, летящая перпендикулярно стержню и его оси. После удара стержень отклонился на угол α = 60o. Определить скорость пули.
161. Определить напряженность G гравитационного поля на высоте h = 1000 км над поверхностью Земли. Считать известными ускорение g свободного падения у поверхности Земли и её радиус R.
162. Какая работа А будет совершена силами гравитационного поля при падении на Землю тела массой m= 2 кг: 1) с высоты h= 1000 км; 2) из бесконечности?
163. Из бесконечности на поверхность Земли падает метеорит массой m = 30 кг. Определить работу А, которая при этом будет совершена силами гравитационного поля Земли. Ускорение свободного падения g у поверхности Земли и её радиус R считать известным.
164. С поверхности Земли вертикально вверх пущена ракета со скоростью v = 5 км/с. На какую высоту она поднимется?
165. По круговой орбите вокруг Земли обращается спутник с периодом Т = 90 мин. Определить высоту спутника. Ускорение свободного падения g у поверхности Земли и её радиус R считать известными.
166. На каком расстоянии от центра Земли находится точка, в которой напряженность суммарного гравитационного поля Земли и Луны равна нулю? Принять, что масса Земли в 81 раз больше массы Луны и что расстояние от центра Земли до центра Луны равно 60 радиусам Земли.
167. Спутник обращается вокруг Земли по круговой орбите на высоте h = 520 км. Определить период обращения спутника. Ускорение свободного падения g у поверхности Земли и её радиус R считать известными.
168. Определить линейную и угловую скорости спутника Земли, обращающегося по круговой орбите на высоте h = 1000 км. Ускорение свободного падения g у поверхности Земли и её радиус R считать известными.
169. Какова масса Земли, если известно, что Луна в течение года совершает 13 обращений вокруг Земли и расстояние от Земли до Луны равно 3,84·108 м?
170. Во сколько раз средняя плотность земного вещества отличается от средней плотности лунного? Принять что радиус Rз Земли в 390 раз больше радиуса Rл Луны и вес тела на Луне в 6 раз меньше веса тела на Земле.
171. На стержне длиной l= 30 см укреплены два одинаковых грузика: один – в середине стержня, другой – на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период T простых гармонических колебаний данного физического маятника. Массой стержня пренебречь.
172. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых x = A1sin(ω1t) и y = A2cos(ω2t), где A1 = 8 см, A2 = 4 см,
173. Точка совершает простые гармонические колебания, уравнения которых x = A sin ωt, где А = 5 см, ω = 2 c-1. В момент времени, когда точка обладала потенциальной энергией
174. Определить частоту ν простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.
175. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
176. Определить период Т колебаний математического маятника, если его модуль максимального перемещения Δr = 18 см и максимальная скорость vmax = 16 см/с.
177. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение x0 = 4 см, а скорость v0 = 10 см/с. Определить амплитуду А и начальную фазу φ0 колебаний, если их период Т =2 с.
178. Складываются два колебания одинакового направления и одинакового периода: x1=A1sinω1t и x2=A2sinω2(t+τ), где А1=А2=3см, ω1=ω2=πс2, τ=0,5с. Определить амплитуду А и начальную фазу φ0 результирующего колебаний. Написать его уравнение. Построить векторную диаграмму для момента времени t=0.
179. На гладком горизонтальном столе лежит шар массой М=200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью k=500 Н/м. В шар попадает пуля массой m=10 г, летящая со скоростью v=300 м/с, застревает в нем. Пренебрегая перемещением шара во время удара и сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.
180. Шарик массой m = 60 г колеблется с периодом Т = 2 с. В начальный момент времени смещение шарика х0 = 4,0 см и он обладает энергией Е = 0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возвращающей силы с течением времени.