


Рассмотрим твёрдое тело массы \( m \), подвешеное и закрепленое шарнирно в одной точке (Рисунок). Момент инерции тела относительно оси вращения \( J \), а его центр тяжести расположен на расстоянии \( a \) от оси, проходящей через точку закрепления. Если твёрдое тело отклонить от положения равновесия, то оно начнёт раскачиваться из стороны в сторону. Такое устройстов называется физический маятник. Физический маятник колеблется по тому же принципу, что и математический маятник. Найдём период колебаний маятника.
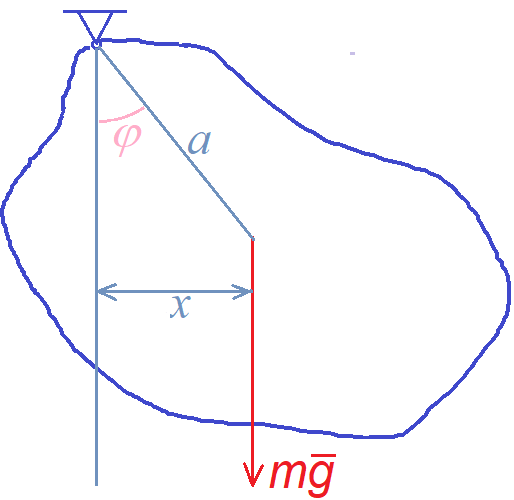
Рисунок 1.
Период колебаний — это время, за которое совершается одно полное колебание. Груз возвращается в исходное положение, с которого началось это колебание.
Для того, чтобы составить дифференциальное уравнение колебаний рассмотрим равновесие моментов сил, приложенных к твёрдому телу. Это сила тяжести \( m \vec g \), приложенная к центру масс маятника. Сила тяжести создаёт момент относительно оси, проходящей через точку подвеса, который стремится вернуть физический маятник в исходное положение равновесия.$$M = -m g x = -m g a sin \varphi \, .$$Здесь \( \varphi \) — угол отклонения прямой, соединяющей центр масс груза с шарниром, от вертикали или от положения равновесия;
Силы реакции опоры, возникающие в шарнире, не создают моментов относительно оси вращения, так как плечо в этом случае равно нулю.
Основное уравнение динамики вращательного движения$$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad M = J \varepsilon \, , \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (1)$$где \( \varepsilon = d^2 \varphi / dt^2 = \ddot \varphi \) — угловое ускорение, которое равно второй производной от угла отклонения \( \varphi \) .
Подставим выражение для углового ускорения физического маятника и момента силы тяжести в уравнение (1). Получим$$-m g a sin \varphi = J \ddot \varphi \, .$$Перенесём в одну сторону и поделим на момент инерции маятника$$\ddot \varphi + {{mga} \over J} sin \varphi = 0 \, .$$
Будем считать, что физический маятник отклоняется от положения равновесия на достаточно малые углы такие, что можно принять приближённое равенство \( sin \varphi \approx \varphi \). Тогда последнее уравнение можно записать в виде$$\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ddot \varphi + \omega^2 \varphi =0 . \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (2)$$Здесь величина$$\omega = \sqrt {{mga} \over J } \, $$есть циклическая частота физического маятника.
Уравнение (2) есть дифференциальное уравнение колебаний физического маятника.
Легко убедиться, что функция$$\varphi (t)=Bcos \omega t+C sin \omega t$$является решением дифференциального уравнения (2) при любых значения величин \(B\) и \(C\). Для определения
произвольных постоянных \(B \) и \(C\) используются начальные условия. Это решение называется общим решением дифференциального уравнения (2).
Как видим, при малом отклонении, угол отклонения меняется по гармоническому закону, то есть физический маятник совершает гармонические колебания. Чтобы определить период колебаний физического маятника заметим, что период синуса и косинуса равен \(2\pi\). Следовательно, период колебаний \(T\) можем определить из условия \(\omega T =2\pi\). Отсюда период колебаний маятника равен$$T ={{2\pi} \over \omega} \,.$$Подставляя выражение для циклической частоты \(\omega\) получим период колебаний физического маятника
$$ T =2\pi \cdot \sqrt { J \over {mga}} \,.$$ В качестве физического маятника рассмотрим, например, стержень длины \(l\) и массы \(m\), подвешенный за один конец. Момент инерции стрежня относительно его середины равен$$J_0 = {{ml^2}\over {12}} \, .$$
Согласно теореме Штейнера, момент инерции стержня относительно оси вращения$$J=J_0 +ma^2 = {{ml^2}\over {12}} + m\left( l\over 2 \right)^2 = {{ml^2}\over {3}}\, .$$
Так как расстояние от центра масс стержня до точки подвеса, то есть до конца стержня, равно \( a=l/2\).
Следовательно, период колебаний маятника равен$$T =2\pi \cdot \sqrt {\left( {{ml^2}\over 3} \right) : \left( {mg{l \over 2}}\right)} = 2\pi \cdot \sqrt {{2l} \over {3g}}\, .$$

| Математический маятник | Физический маятник | Пружинный маятник | Крутильный маятник |
| Колебания груза в полусфере | Колебания стержня на цилиндре | Колебания буя на воде |