
Задача 7. Исследовать на сходимость ряд.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
7.13. Исследовать на сходимость ряд.
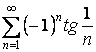
Решение.
Рассмотрим ряд, составленный из модулей 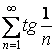 . Общий член ряда
. Общий член ряда  . Сравним этот ряд с гармоническим рядом
. Сравним этот ряд с гармоническим рядом 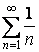 .
.
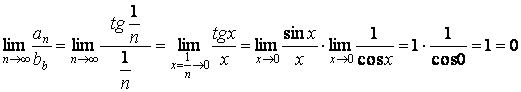
По предельному признаку сравнения, оба ряда сходятся или расходятся одновременно. Но гармонический ряд расходится. Следовательно, ряд

тоже расходится.
Рассмотрим исходный знакочередующийся ряд 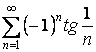 . Заметим, что
. Заметим, что
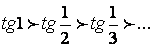
 .
. Ряд удовлетворяет условиям теоремы Лейбница, поэтому ряд сходится. Следовательно, исходный ряд сходится условно.
Ответ: Ряд сходится условно.