
Задача 4. Исследовать на сходимость ряд.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
Исследование сходимости ряда в данном задании основано на признаке Д’Аламбера (не путать с Д’Артаньяном).
Признак Д’Аламбера. Если в ряде с положительными членами
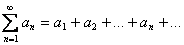
отношение n+1 –го члена к n – му при n → ∞ имеет конечный предел q, то есть
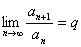 ,
, то: ряд сходится, в случае если q < 1 и ряд расходится, в случае если q > 1.
Примечание: Если q = 1, то ответа на вопрос о сходимости ряда или расходимости ряда теорема не даёт. В этом случае сходимость ряда не определяется при помощи признака Д'Аламбера.
4.12. Исследовать на сходимость ряд
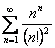 .
.Решение.
Общий член ряда
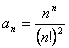 .
.Чтобы исследовать сходимость ряда при помощи признака Д'Аламбера нам понадобится последующий член ряда, который получается заменой n на n+1. То есть
 .
.Вычислим предел
 .
. Так как q = 0 < 1, то по признаку Д’Аламбера ряд сходится.
Ответ: Ряд сходится.