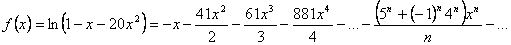Задача 14. Разложить функцию в ряд Тейлора по степеням.
Внимание! Условия задачи 14 соответсвуют номерам из задачи 19 старого издания. Пожалуйста, не обращайте внимание на номер в начале задачи, сверяйте только само задание. Это действительно задача 14 из сборника Кузнецова 2005 года.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
14.28. Разложить функцию 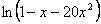 в ряд Тейлора по степеням x.
в ряд Тейлора по степеням x.
Найдём корни квадратного трёхчлена 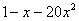 , решая уравнение
, решая уравнение 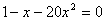 или
или  . Дискриминант квадратного уравнения
. Дискриминант квадратного уравнения 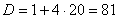 . Тогда корни
. Тогда корни
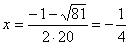 ,
, 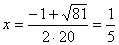 .
.Квадратный трёхчлен запишется
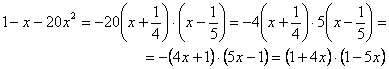
Тогда, с учётом того, что логарифм произведения равен сумме соответствующих логарифмов, функция примет вид
 .
. Воспользуемся разложением функции 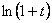 в ряд Маклорена по степеням t
в ряд Маклорена по степеням t
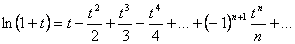
При t = 4x, получим
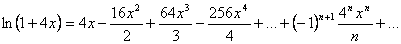
При t = −5x, получим
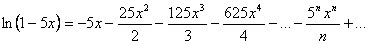
Подставим полученные ряды в выражение для 

После приведения подобных слагаемых получим ряд Тейлора по степеням x
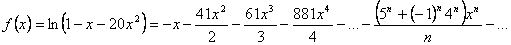
Ответ: