
Задача 16. Вычислить площади фигур, ограниченных линиями, заданными уравнениями в полярных координатах.
Введите номер своего варианта или решите задачу по образцу, приведённому ниже.
16.8. Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах 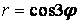 .
.
Решение.
Эта фигура называется трёхлепестковой розой. Она состоит из трёх одинаковых лепестков.

Область определения 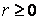 или
или 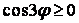 . Отсюда
. Отсюда 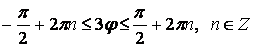 или
или 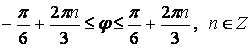 .
.
Один лепесток определяется
углами 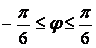 . Площадь одного лепестка
. Площадь одного лепестка
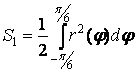
Подставим выражение для радиуса и получим площадь одного лепестка
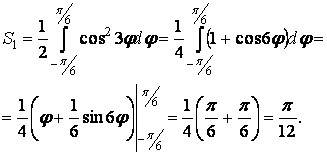
Тогда площадь трёхлепестковой розы
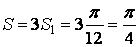
Итак, мы нашли площадь фигуры, заданной в полярных координатах.
Ответ: 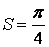 .
.