

Если у вас нет времени и вам нужно решить математику, то наш сайт именно для вас. Мы решаем задачи по математике — решаем математику. Решаем задачи из любых разделов математики.
Заказать решение задачи по математике можно кликнув по красной кнопке ниже или написав запрос по электронному адресу  .
.
У нас очень справедливые расценки и комфортное обслуживание. Мы стремимся создать у наших клиентов положительный опыт общения с математикой.
Напишите письмо прямо сейчас и узнайте стоимость вашего заказа.
Заказывайте решение математики прямо сейчас и договаривайтесь о скидке.

Так как же решить математику?
Этот вопрос рано или поздно встаёт перед любым студентом. Некоторым студентам математика даётся легко, другим значительно труднее. Но преподаватели математики неумолимы, они не делают скидку на сложность понимания и предъявляют ко всем студентам одинаковые требования. Оно и правильно, ведь если предъявлять разным студентам разные требования в вопросах решения математики, то это будет выглядеть не очень благовидно, и вызовет недоумение у самих студентов. А любой преподаватель, если он настоящий преподаватель, а не коррумпированный оборотень у доски, дорожит мнением своих студентов и старается предъявлять ко всем студентам одинаковые требования. Это называется объективностью. И, тем не менее, реальность такова, что счастливчики, оказавшиеся на студенческой скамье, имеют разный уровень познания в математике и разные способности в решение задач. Что делать тем, кто не очень хорошо подкован в математике, но очень хочет получить заветную корочку и обрести нужные навыки в выбранной профессии.
На нашем сайте огромное количество готовых решений из разных сборников. Вы можете бесплатно решить задачу по математике или научиться решать задачи. Если у вас нет времени учиться, то кликнув красную кнопку ниже, вы получите в бесплатное пользование огромный арсенал уже решённых задач.

На нашем сайте есть множество учебных материалов, позволяющих самостоятельно решить математику. Имеется огромное количество образцов решения математических задач. Ищите и обрящете.
Ниже несколько примеров того, как можно решить задачу по математике.
Вычислить предел числовой последовательности
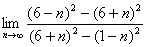
Решение.
Раскроем скобки и приведём подобные:

Вынесем 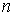 за скобки и сократим. Получим
за скобки и сократим. Получим
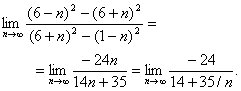
Воспользуемся теоремой о пределе суммы, разности и частного последовательностей:
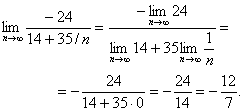
Ответ:
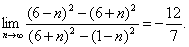
Найти асимптоты и построить график функций.
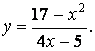
Решение.
1) Область определения функции
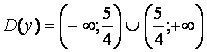
2) Функция ни четная, ни нечетная.
3) Функция непрерывна во всех точках области определения
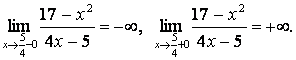 .
. Следовательно, точка 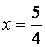 - точка разрыва второго рода. Прямая
- точка разрыва второго рода. Прямая 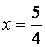 является вертикальной асимптотой.
является вертикальной асимптотой.
4) Найдём наклонную асимптоту 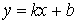 .
.
Здесь
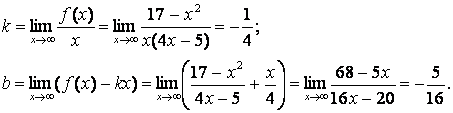
Следовательно, наклонная асимптота имеет уравнение
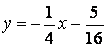 .
. 5) Найдём производную
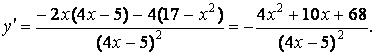
Производная нигде не обращается в ноль и всюду отрицательная. Следовательно, функция убывает во всей области определения.
6) Найдем точки пересечения с осями.
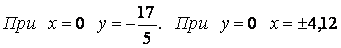 .
.7) Построим график.
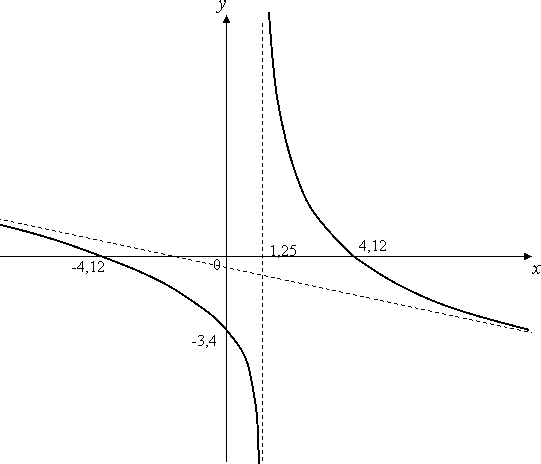
Вычислить определённый интеграл
 .
.Решение.
Сделаем замену: 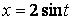 . Тогда
. Тогда 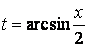 и
и
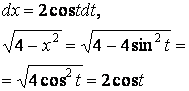
Пределы интегрирования:

Интеграл запишется:
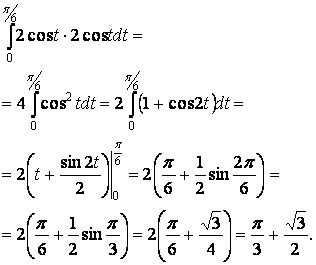
Ответ: 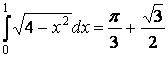 .
.
Пусть 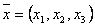 . Являются ли линейными следующие преобразования:
. Являются ли линейными следующие преобразования:
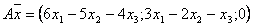
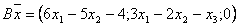
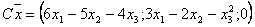
Решение.
Преобразование 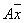 является линейным, так как оно может быть представлено в виде произведения матрицы
является линейным, так как оно может быть представлено в виде произведения матрицы
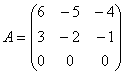
и столбца координат вектора
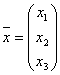
А такое произведение обладает свойствами линейности, ведь это произведение матриц. То есть
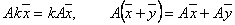
Преобразование 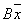 не является линейным.
не является линейным.
Действительно
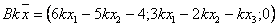 ,
, а
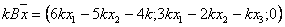 ,
, и, следовательно, 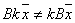 . То есть, одно из свойств линейности не выполняется. Поэтому преобразование нелинейное.
Преобразование
. То есть, одно из свойств линейности не выполняется. Поэтому преобразование нелинейное.
Преобразование 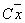 не является линейным.
не является линейным.
Действительно
 ,
, а
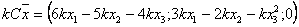 ,
, и, следовательно, 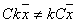 . То есть, одно из свойств линейности не выполняется. Поэтому преобразование нелинейное.
. То есть, одно из свойств линейности не выполняется. Поэтому преобразование нелинейное.
Ответ: Преобразование 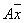 является линейным, а преобразования
является линейным, а преобразования 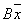 и
и 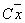 нелинейные.
нелинейные.
Решить смешанную задачу
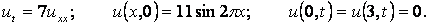 .
.Решение.
Это уравнение теплопроводности. Решаем задачу по методу Фурье.
Решение имеет вид:
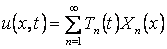
Здесь 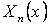 — собственные функции задачи Штурма-Лиувилля с условиями, соответствующими рассматриваемым граничным условиям;
— собственные функции задачи Штурма-Лиувилля с условиями, соответствующими рассматриваемым граничным условиям;
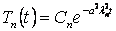
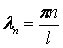 - собственные значения задачи Штурма-Лиувилля;
- собственные значения задачи Штурма-Лиувилля; 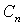 — коэффициенты, определяемые по начальным условиям.
— коэффициенты, определяемые по начальным условиям.
Cобственные функции задачи Штурма-Лиувилля

Таким образом, решение исходной задачи имеет вид
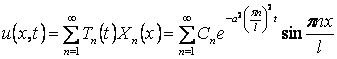
В частности, при 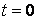 получим
получим
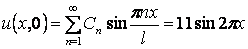
В нашем случае 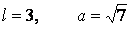 и
и

В последнем равенстве, слева стоит разложение функции 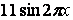 в ряд Фурье.
в ряд Фурье.
Коэффициенты ряда Фурье
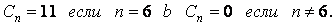 .
.
Таким образом,
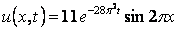 .
.Ответ:
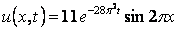 .
. Надеемся, эта статья была вам полезна и теперь вы знаете, что нужно сделать чтобы решить математику без лишних хлопот.

Физика для студентов заочной формы обучения
Высшая математика: Ответы на вопросы к экзамену
МАТЕМАТИКА ЗАОЧНИКАМ